Embark on a geometric adventure with our “Chords and Arcs Quick Check”! This exploration delves into the fascinating world of chords and arcs, uncovering their definitions, properties, and practical applications. Brace yourself for a journey filled with clarity and intrigue as we unravel the secrets of these geometric elements.
In this comprehensive guide, we’ll define chords and arcs, showcasing their intricate relationship through diagrams and examples. We’ll delve into the properties of chords, including central chords, and arcs, including semicircles. Discover the connection between chord length and intercepted arc measure, empowering you with the tools to navigate geometric challenges with ease.
Definitions of Chords and Arcs: Chords And Arcs Quick Check
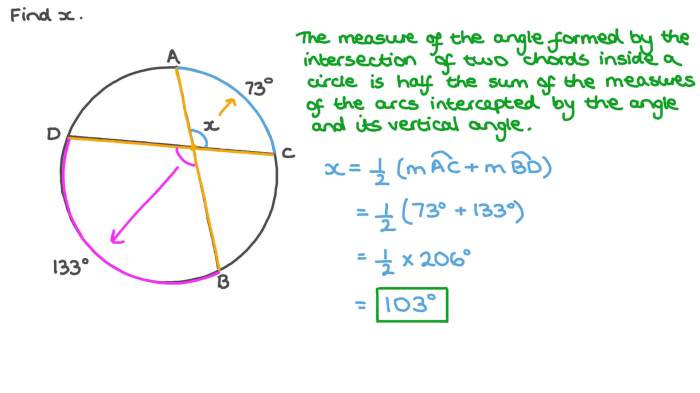
In geometry, a chord is a line segment that joins two points on a circle. An arc is a part of a circle that is bounded by two radii.
For example, in the diagram below, the line segment AB is a chord, and the arc AB is the part of the circle that is bounded by the radii OA and OB.
The chords and arcs quick check is a valuable tool for assessing understanding of these concepts. If you’re looking for further reading, check out the a&p john updike full text . It provides an in-depth exploration of these ideas and can help you deepen your knowledge of chords and arcs.

The length of a chord is equal to the diameter of the circle multiplied by the sine of half the angle that the chord subtends at the center of the circle.
The measure of an arc is equal to the angle that the arc subtends at the center of the circle.
Properties of Chords and Arcs

Chords and arcs are two fundamental geometric shapes that are closely related to circles. A chord is a line segment that connects two points on a circle, while an arc is a part of a circle’s circumference that is bounded by two radii.
In this section, we will explore the properties of chords and arcs, including the relationship between their lengths and measures.
Properties of Chords
- A chord divides a circle into two regions, called segments.
- The perpendicular bisector of a chord passes through the center of the circle.
- The length of a chord is always less than the diameter of the circle.
- A chord that passes through the center of a circle is called a diameter.
- The diameter of a circle is the longest chord that can be drawn in the circle.
Properties of Arcs
- An arc is a part of a circle’s circumference that is bounded by two radii.
- The measure of an arc is the angle formed by the two radii that bound it.
- The measure of an arc is always less than 360 degrees.
- An arc that measures 180 degrees is called a semicircle.
- A semicircle is the largest arc that can be drawn in a circle.
Relationship between the Length of a Chord and the Measure of its Intercepted Arc
The length of a chord and the measure of its intercepted arc are related by the following formula:“`length of chord = 2
- radius
- sin(1/2
- measure of arc)
“`This formula can be used to find the length of a chord given the measure of its intercepted arc, or to find the measure of an arc given the length of its intercepted chord.
Measuring Chords and Arcs

In geometry, measuring the length of chords and the measure of arcs is crucial for understanding circles. Let’s explore how to calculate these measurements.
Length of a Chord
The length of a chord can be determined using the Pythagorean theorem. Given a chord with endpoints (x 1, y 1) and (x 2, y 2), its length is calculated as:
Length of Chord = √((x2
- x 1) 2+ (y 2
- y 1) 2)
For instance, if a chord has endpoints (3, 4) and (6, 8), its length is √((6 – 3) 2+ (8 – 4) 2) = √(3 2+ 4 2) = √(9 + 16) = √25 = 5 units.
Measure of an Arc, Chords and arcs quick check
The measure of an arc is the length of the arc on the circle’s circumference. It is expressed in degrees or radians. To find the measure of an arc, we use the following formula:
Measure of Arc = (Length of Arc / Circumference of Circle) × 360°
Or, in radians:
Measure of Arc = (Length of Arc / Circumference of Circle) × 2π
For example, if an arc has a length of 6 cm and the circumference of the circle is 12 cm, its measure is (6 cm / 12 cm) × 360° = 180°. In radians, it would be (6 cm / 12 cm) × 2π ≈ 3.14 radians.
Applications of Chords and Arcs

Chords and arcs are fundamental geometric concepts with numerous practical applications in various fields, particularly architecture and engineering. Understanding these concepts is crucial for professionals in these domains.
Architecture
In architecture, chords and arcs play a vital role in designing and constructing various structural elements. For instance, arches are commonly used in bridges, buildings, and other structures to create openings and support weight. The shape and dimensions of the arch are determined by the length of the chord and the radius of the arc.
Additionally, chords and arcs are used in designing domes, vaults, and other curved architectural features.
Engineering
In engineering, chords and arcs are essential for analyzing and designing bridges, tunnels, and other structures. By understanding the geometric relationships between chords and arcs, engineers can calculate the forces and stresses acting on these structures and ensure their stability and safety.
Additionally, chords and arcs are used in designing gears, cams, and other mechanical components.
Top FAQs
What is a chord in geometry?
A chord is a line segment that connects two points on a circle or an arc.
How do you measure the length of an arc?
The length of an arc can be calculated using the formula: length = (2πr / 360) × degrees of arc, where r is the radius of the circle and degrees of arc is the measure of the intercepted arc in degrees.
What is the relationship between the length of a chord and the measure of its intercepted arc?
The length of a chord is directly proportional to the measure of its intercepted arc. As the length of the chord increases, the measure of the intercepted arc also increases.