Unit 2 dilations similarity and introducing slope – Unit 2: Dilations, Similarity, and Introducing Slope delves into the captivating world of transformations and linear relationships, providing a comprehensive understanding of these fundamental concepts. Through engaging discussions and real-world examples, we will explore the properties of dilations, the connections between similarity and congruence, and the significance of slope in understanding linear relationships.
As we journey through this unit, we will uncover the practical applications of dilations in architecture and engineering, and delve into the everyday uses of slope in construction and physics. Prepare to be enthralled as we unravel the mysteries of transformations and linear relationships, empowering you with a deeper understanding of the mathematical world around us.
Understanding Dilations
Dilations are geometric transformations that enlarge or reduce a figure by a certain factor while maintaining its shape. The center of dilation is the fixed point around which the figure is enlarged or reduced.
Dilations are commonly used in architecture, engineering, and other fields where it is necessary to enlarge or reduce a design while maintaining its proportions.
Properties of Dilations
- The scale factor of a dilation is the ratio of the length of the corresponding sides of the original and dilated figures.
- The center of dilation is the point that remains fixed during the dilation.
- Dilations preserve angles and parallel lines.
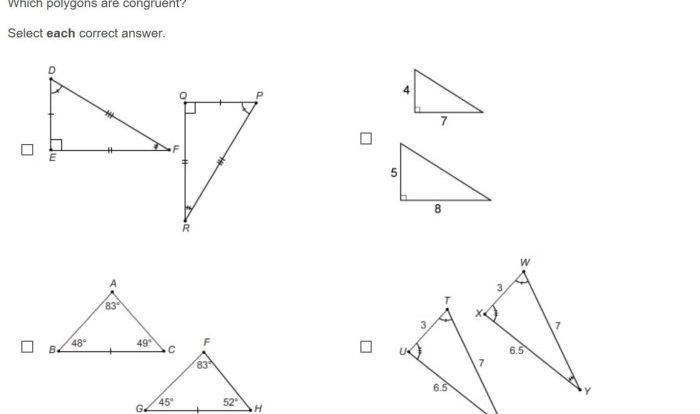
Similarity and Congruence: Unit 2 Dilations Similarity And Introducing Slope

Similarity
Similar figures have the same shape but not necessarily the same size. The scale factor between two similar figures is the ratio of their corresponding side lengths.
Congruence
Congruent figures have the same shape and size. They are identical in every way, including their corresponding side lengths and angles.
Relationship between Similarity and Dilations
Dilations can be used to create similar figures. When a figure is dilated by a scale factor of 1, the resulting figure is congruent to the original figure.
Introducing Slope
Slope is a measure of the steepness of a line. It is defined as the ratio of the change in the y-coordinate to the change in the x-coordinate as you move along the line.
Calculating Slope
The slope of a line can be calculated using the following formula:
m = (y2
- y 1) / (x 2
- x 1)
where (x 1, y 1) and (x 2, y 2) are two points on the line.
Significance of Slope, Unit 2 dilations similarity and introducing slope
Slope is an important concept in linear relationships. It can be used to determine the rate of change, predict future values, and solve equations.
Applications of Dilations and Slope
Applications of Dilations
- Architecture: Dilations are used to enlarge or reduce architectural plans while maintaining the proportions of the design.
- Engineering: Dilations are used to scale up or down engineering drawings to fit different specifications.
Applications of Slope
- Construction: Slope is used to determine the angle of a roof or the gradient of a road.
- Physics: Slope is used to calculate the velocity and acceleration of objects.
General Inquiries
What is a dilation?
A dilation is a transformation that changes the size of a figure without changing its shape.
What is the difference between similarity and congruence?
Similar figures have the same shape but not necessarily the same size, while congruent figures have both the same shape and the same size.
What is the formula for slope?
The slope of a line is calculated as the change in y divided by the change in x.